The Scientific AI Research Group

We are a research group at UT Austin led by Dr. Richard Tsai. Our current focus is on developing machine learning approaches that complements the more classical techniques for challenging scientific computing tasks. The types of scientific computing problems that we have considered include time-parallelizable multiscale coupling algorithms for initial value problems, nonlinear interface dynamics, partial differential equations on surfaces, multiscale modeling, wave propagation, optimal transport, sensor networks, robotic path planning problems. Our research are supported by National Science Foundation and the Army Research Office.
Recent News
People
Faculty:
Postdocs:
Axel G TurnquistGraduate Students:
Rui Fang
Lewis Liu
Lukas Taus
Luis Kaiser
(Some previous photos of group members and activities can be found here.)
Papers
A collection of selected papers can be found here.
Access to codes of some of our projects
- Numerical Wave Propagation Aided by Deep Learning:
- Click Here to get the training databases.
- Click Here to get the tutorial notebooks for the project.
Projects
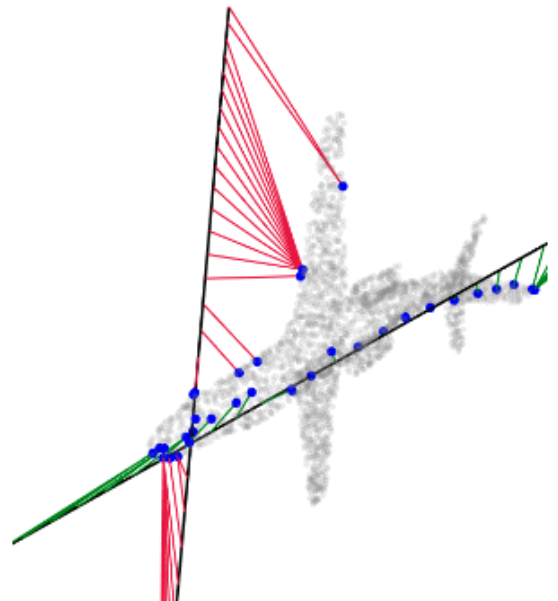
Sampling and Processing of Point Clouds
We propose a new framework for the sampling, compression, and analysis of distributions of point sets embedded in Euclidean spaces. Our approach involves constructing a tensor called the RaySense sketch, which captures nearest neighbors from the underlying geometry of points along a set of rays.
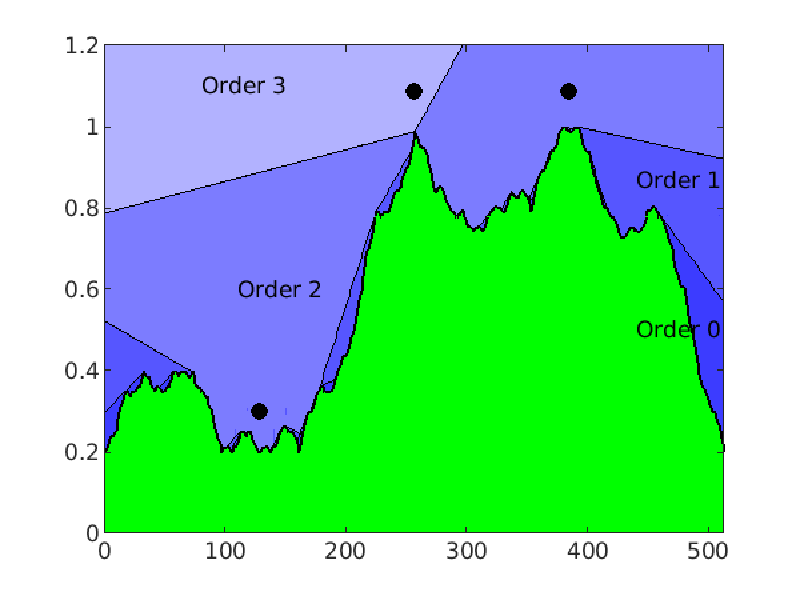
Optimizing Sensor Network Design for Multiple Coverage
We introduce a new objective function for the greedy algorithm to design efficient and robust sensor networks and derive theoretical bounds on the network's optimality. We further introduce a Deep Learning model to accelerate the algorithm for near real-time computations. Correspondingly, we show that understanding the geometric properties of the training data set provides important insights into the performance and training.

Impact of the Extrinsic Geometry on Linear Regression
We study linear regression applied to data structured on a manifold. Our objective is to reveal the impact of the data manifold's extrinsic geometry on the regression.
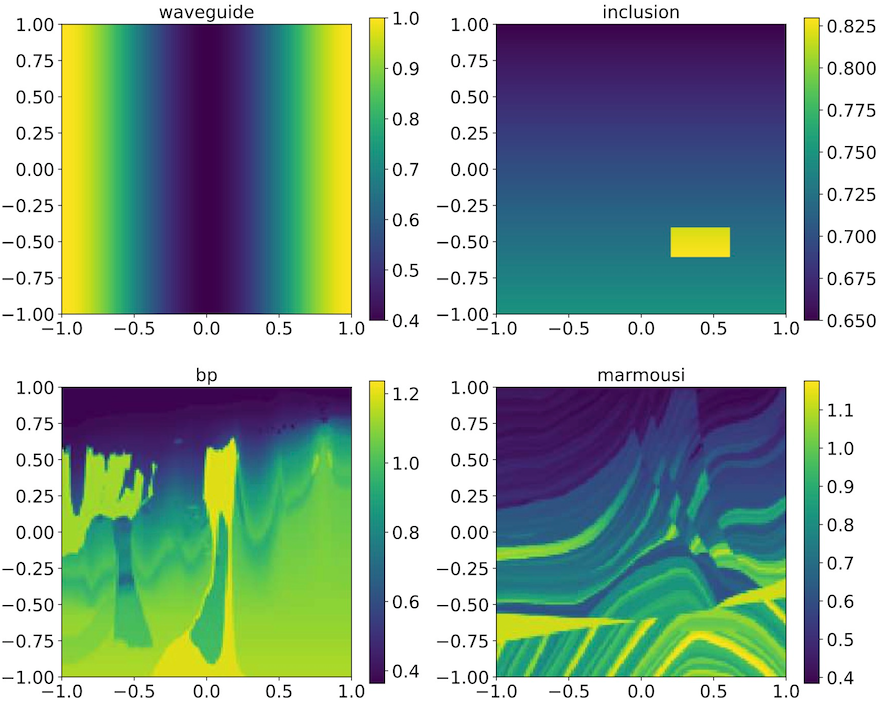
Numerical Wave Propagation Aided by Deep Learning
We propose a deep learning approach for wave propagation in media with multiscale wave speed, using a second-order linear wave equation model.
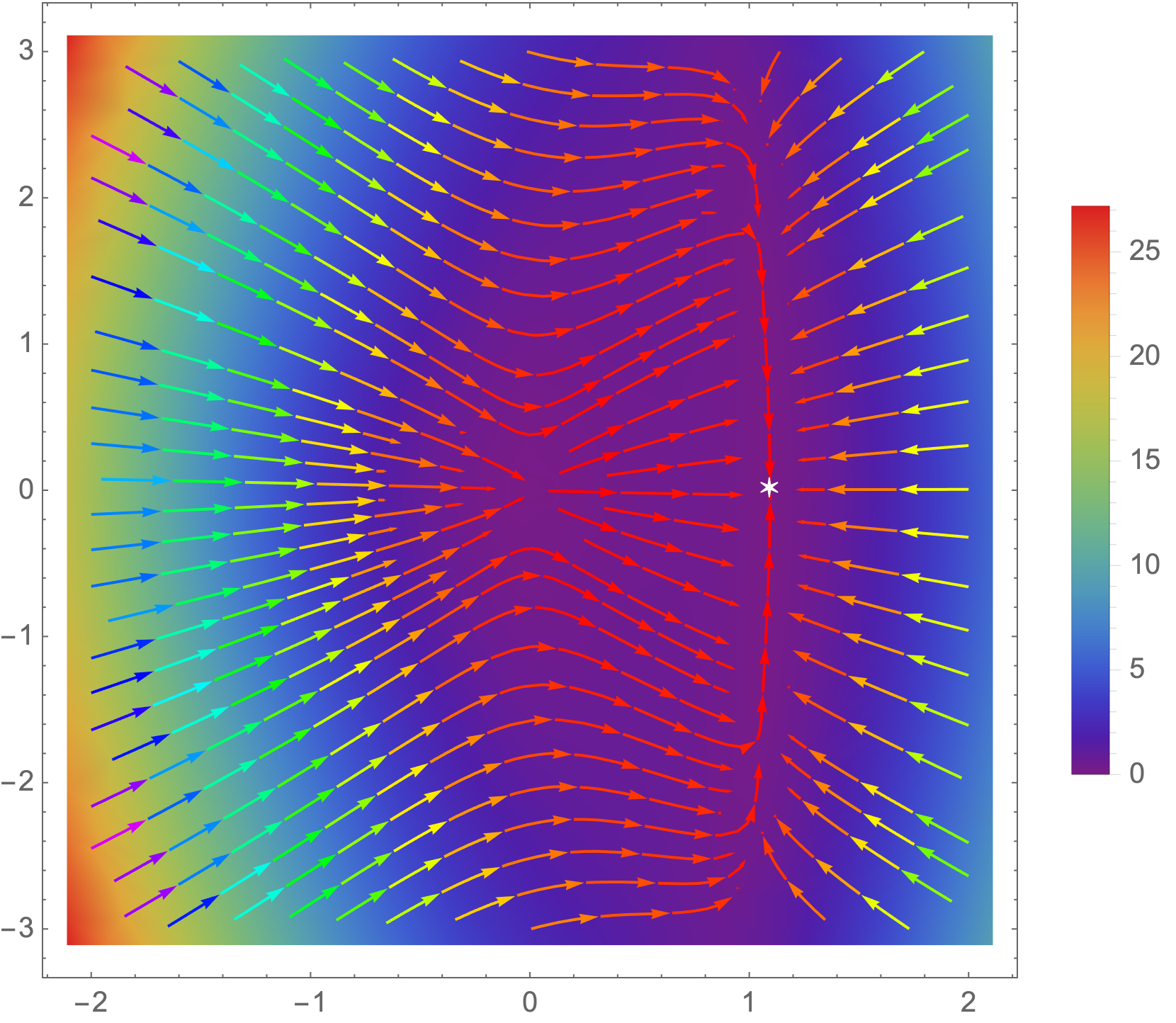
Deep learning and the Low Dimensional Manifold Hypothesis
We study how the low dimensional manifold hypothesis of data will interact with deep learning models.

Multiscale coupling algorithms using parareal style structures
We are developing a data-driven parallel-in-time iterative method to solve the homogeneous second-order wave equation.
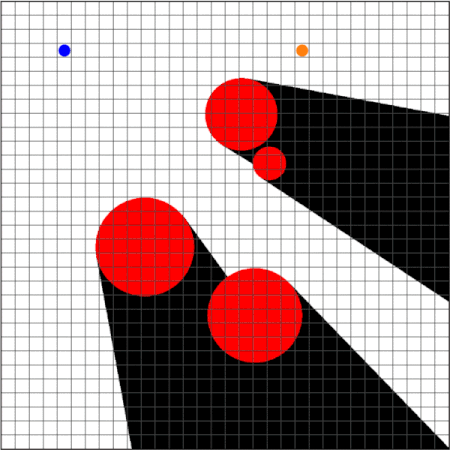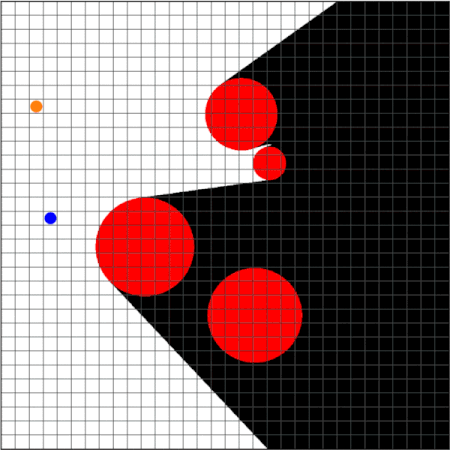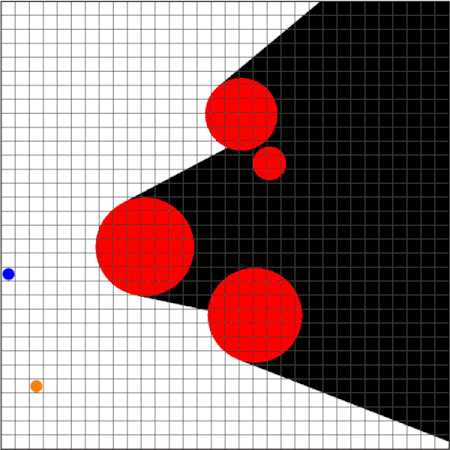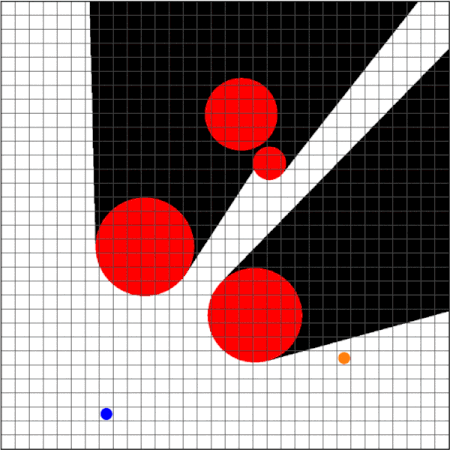
Strategy Synthesis for Surveillance-Evasion Games with Learning-enabled Visibility Optimization
We study a two-player game with a quantitative surveillance requirement on an adversarial target moving in a discrete state space and a secondary objective to maximize short-term visibility of the environment.

AI-enabled Exploration and Surveillance
We develop a new state-of-the-art deep learning strategy for prescribing vantage points for optimal sensor placement. This approach uses a robust volumetric visibility computation to efficiently model arbitrary geometries.
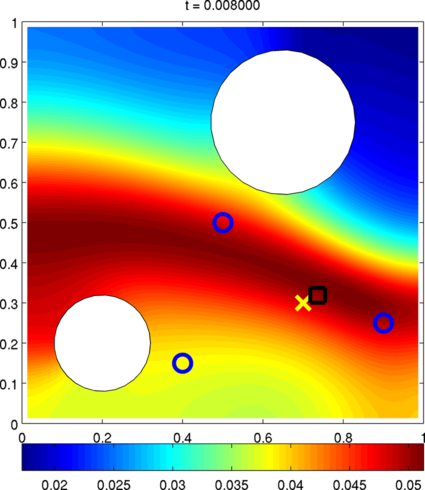
Point source identification in non-linear advection-diffusion-reaction systems
We consider a problem of identification of point sources in time dependent advection-diffusion systems with a non-linear reaction term.
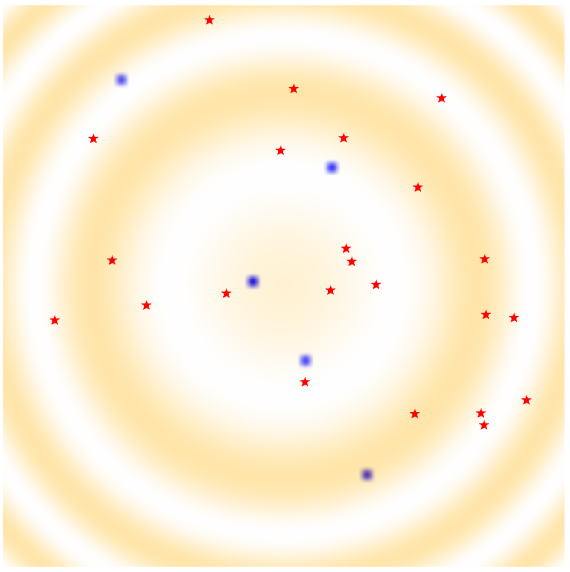
Heat Source Identification Based on L1 Constrained Minimization
We consider the inverse problem of finding sparse initial data from the sparsely sampled solutions of the heat equation. The initial data are assumed to be a sum of an unknown but finite number of Dirac delta functions at unknown locations.